This post has been republished on Economy Politics. Economy Politics is a blog published by Taylor Cottam. We would like to welcome Taylor as a contributing author to InvestingThesis. We’ve interviewed Taylor before but for some background, Taylor has managed financial risk and traded fixed income products inside both GMAC bank and other financial institutions in Europe, North America and Canada. He is also the author of numerous business and economic articles, is a CFA Charterholder, a Certified Financial Risk Manager (FRM) and holds an MBA from INSEAD.
Update: This article was included in the 265th Carnival of Personal Finance posted at Funny about Money .
I was talking with a friend who was telling me that it was the absolute perfect time to buy a house because housing prices have tumbled and interest rates are low.
I asked him, “What happens to housing prices if there is inflation and rates go up?”
“Housing prices should go up with inflation as they do for all goods. Housing is a natural hedge for inflation”
Did my friend have a point? Yes and no.
Yes, he was right that in a high inflationary environment, housing prices should rise with all other assets. Rents will go up, as will the price of all the inputs into housing such as lumber and labor costs.
Obviously, housing prices will go up to reflect this reality.
But no, when inflation and thus nominal interest rates increase, housing prices tumble. When rates fall, housing prices tend to increase.
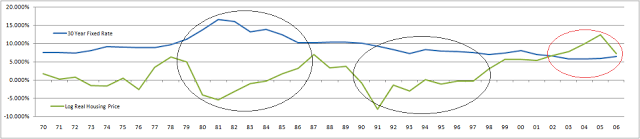
Relationship between mortgage rates and housing prices
You can see an obvious correlation by looking at the following graph of interest rates and the log of real housing. The two black circles are areas where the correlation is obvious. The third red circle is an area where the correlation seems less relevant.
The simplest explanation for this correlation comes down to payment. Most people have to finance their homes. As such, they make housing decision based upon monthly payment, i.e. what they can afford. If a borrower with 2,000.00 available per month for a mortgage, they could afford to finance about $372,500 over 30 years with a 5% rate. If that rate were to increase to 10%, the amount they could afford to finance would drop by almost 40% to $273,000.
From 1982 to 2003, there was a long term trend of dropping mortgage rates. During this same term, we had a general improvement in the change in housing prices. The exception was 1990 to 1991 where there is a period of negative changes to housing prices that aren’t explained by the mortgage rates. Also, from 2003 to 2006, mortgage rates stabilized, but housing increased dramatically. New products such became popular such as subprime mortgages and payment option arms that allowed lower payments so people could afford more housing and thus drive up the price even while mortgage rates were stable.
But just how quickly do prices react to changes in interest rates?
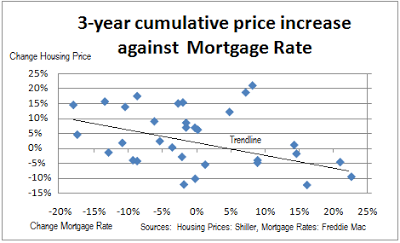
We did a regression analysis of interest rates and real housing prices over the last thirty years. When we do a year over year analysis while looking at the change of real housing prices over the same timeframe, we get no correlation (see table). When we took a look at the data with a lag, we get more interesting results.
For the mortgage rate information I am using Freddie Mac 30 year fixed mortgage rates. I am taking the average rate over the course of one calendar year. I use the change (or log) of the mortgage rate in the regression. Because it is averaged, the functional rate is close to the middle of the year. For housing data, I am use beginning-of-year real housing pricing data from Shiller. Then I take the change (or log) of this figure. Keep in mind that we are looking at real housing prices less inflation. If you looked at nominal rates in a high inflationary environment, prices might be nominally stagnant, but the real prices might actually have dropped.
As we are using middle of the year mortgage rate data and beginning of year housing data, a 1 year lag in the data is actually closer to a 6 month lag. And a comparison of year to year data would be middle of year mortgage data with beginning of year housing data. Thus, a comparison of year to year data should be statistically insignificant and that is exactly what the results show.
There are other reasons to believe that the changes to the interest rates would not immediately transfer to home prices. Indeed, we found that the lag could be up to three years (2 ½ years). This could be partially explained by the following:
- Real Estate market is illiquid as selling a home can take several weeks if not months.
- Appraisal values are based upon sales price comparisons which can be several months old.
- Financing a purchase of a home could be difficult if sale value is significantly above appraisal value
- Individuals may be inclined to wait rather than sell if the neighbouring homes sold for more.
With a one, two and three year time lag, all give us significant results at the 90% level. Only year two gives us significant results at the 95% level. Year 1 and Year 3 are very close to the threshold of being significant at the 95% level.
| Years | Housing Lag | Coefficient | Intercept | R^2 (% Explained) | Significant at 95% | Significant at 90% |
| 1972–2006 | No Lag | -0.022 | 0.018 | 0.002 (0.2%) | No | No |
| 1972–2005 | 1 year | -0.149 | 0.018 | 0.109 (10.9%) | No | Yes |
| 1972–2004 | 2 years | -0.182 | 0.018 | 0.174 (17.4%) | Yes | Yes |
| 1972–2003 | 3 years | -0.142 | 0.021 | 0.103 (10.3%) | No | Yes |
Regression Analysis
The coefficient is the calculation that would be used to forecast housing price changes based solely upon interest rates. For example, using a housing lag of 2 years (1 ½ years ), if today there were a 100% increase in mortgage rates (5% to 10%), we would expect a housing drop of 16.6% (-.182+.018) in year 2. The R-squared is the percentage of the change that is explained by the mortgage rate change. If R-squared were 1.00, then 100% of the changes to the housing prices are explained by changes in the mortgage rate. A figure of .174 means that less than 20% of the changes of the housing prices are explained by the changes in the mortgage rate. In other words, there is a lot of other factors which combined are even more relevant than just the mortgage rate.
Why is R-squared so low?
The previous graph shows that when there are large changes to the mortgage rate, the relevance is much greater than the R-squared we calculated. Mortgage rates being stable allows other issues dominate. If there were a large scale increase in inflation (say from 1% today to 6% three years from now), that would increase the nominal mortgage rate from about 5% today to 10% credit spreads being equal. The R-squared, or significance would likely shoot way up.
How do we use these numbers?
With an R-squared of .174, less than 20% of the change is explained by the mortgage rate. Consequently, I would not use the coefficients and intercept to forecast when there are small changes in the mortgage rates as other factors would dominate. What I am most concerned about is a large scale increases in inflation and how this would affect real housing prices. In the case of large scale increases, forecasting using the coefficients would be acceptable as the mortgage rate would dominate.
Adding the effect from multiple years
While using the data with a 2 year lag is the only dataset that is relevant at the 95%, years 1, 2 and 3 are relevant at the 90% level. The coefficients and r-squared values suggest that changes to housing prices come slowly over time as a bell curve with the majority of the changes coming in year 2, but significant changes also occur in years 1 and 3.
One way to capture the effect of multiple years would be to simply add the coefficients from years 1, 2 and 3, in which case we would get a coefficient of -0.473. However, given that there are different R-squared and different levels of significance, it would be a challenge to know the level of confidence we would have in our forecasting. Also, I would not be comfortable using data that did not have a higher significance level.
The more proper way to capture multiple years would be to take the product of the changes over three years. If we regress that dataset against the changes in the mortgage rate we get a dataset which captures the effect of a change in the interest rate on multiple years.
| Years | Combined Years | Coefficient | Intercept | R^2 (% Explained) | Significant at 95% | Significant at 90% |
| 1972–2003 | 2 years | -0.268 | 0.023 | 0.155 (15.5%) | Yes | Yes |
| 1972–2003 | 3 year | -0.339 | 0.038 | 0.133 (13.3%) | Yes | Yes |
Current Interest Rate Volatility
But how do we know where the interest rate will be in the future? We can estimate the volatility of the mortgage rate by looking at the history of the 30-year treasury yields. I also looked at different terms 5-year and 10-year and my volatility figures were very similar. When we extrapolate this data into the mortgage rate, we are assuming that credit spreads do not change. We also assume that the change in interest rate is normally distributed, and we realize that the nominal interest rate cannot go below 0%. The annual volatility is 4.22%. This means that there is roughly a 16% probability that the annual mortgage rate will be above 9.22% (5% + 4.22%) one year from now.
| Product | Daily volatility | Monthly Volatility | Annual Volatility |
| 30 year treasury yield | 0.27% | 1.22% | 4.22% |
The big picture
Using these results, we can ask ourselves what is the most that the interest rate could change in a given year. Given the current rates at about 5%, we would be wise to understand the risk to housing given current scenarios (See below). We must remember when discussing these numbers that they are the real housing less inflation. If there was a significant increase in inflation, prices may just stagnate while in real terms they lose 10% a year.
Secondly when dealing with statistics you always have upper and lower bounds which bracket your expected mean. In this case the brackets are quite large. The coefficient has an upper and lower bound 0.30 above and below the expected mean. That means while on the lower end, with 95% accuracy the mortgage rates could have negligible effect, on the higher end, we could have a much higher coefficient than is currently predicted. -0.63.
The intercept value is .038 which means that on average we should expect a 3.8% increase in housing over a 3 year period of time, even if there is no change to the mortgage rate. So when we conduct our scenario analysis, we see that a simple increase in the mortgage rate from 5 to 7.5, we would expect to see a 13% decrease in housing prices over three years. The worst case scenario at 95% would be a 45.8% drop. If inflation really showed its ugly head and rates go to 11.75%, we would expect a 30% drop in real housing prices with a worst case scenario of a 45% drop.
| Scenario | Probability of event | Expected Change | Worst Case at 95% | Timeframe |
| Increase 2.5% in one year | 27.7% | -13.2% | -30.0% | Over 2 ½ years |
| Increase 6.75% over 3 years | 5.0% | -20.9% | -45.8% | Over 5 ½ years |
Conclusion
Given the risk of future inflation, housing is a poor bet at best and a catastrophe at worst. While not wanting to sound alarm bells, the potential on the downside is apparent. On the upside, the real housing prices stay flat but the lower bounds are quite concerning.